Comment Montrer Qu Une Fonction Est Bijective

Définitions - Méthodes - ExemplesL'essentiel à savoir pour montrer qu'une fonction est (ou n'est pas) bijective !

bijective. 2.Pour montrer que g est bijective deux méthodes sont possibles. Première méthode : montrer que g est à la fois injective et surjective. En effet soient n;n02Z tels.

1. Déterminer pour quelles valeurs de (a,b)la fonctionfa,best injective, pour quelles valeurs elle est. surjective. 2. Lorsquefa,best bijective, déterminer son application réciproque. 3..

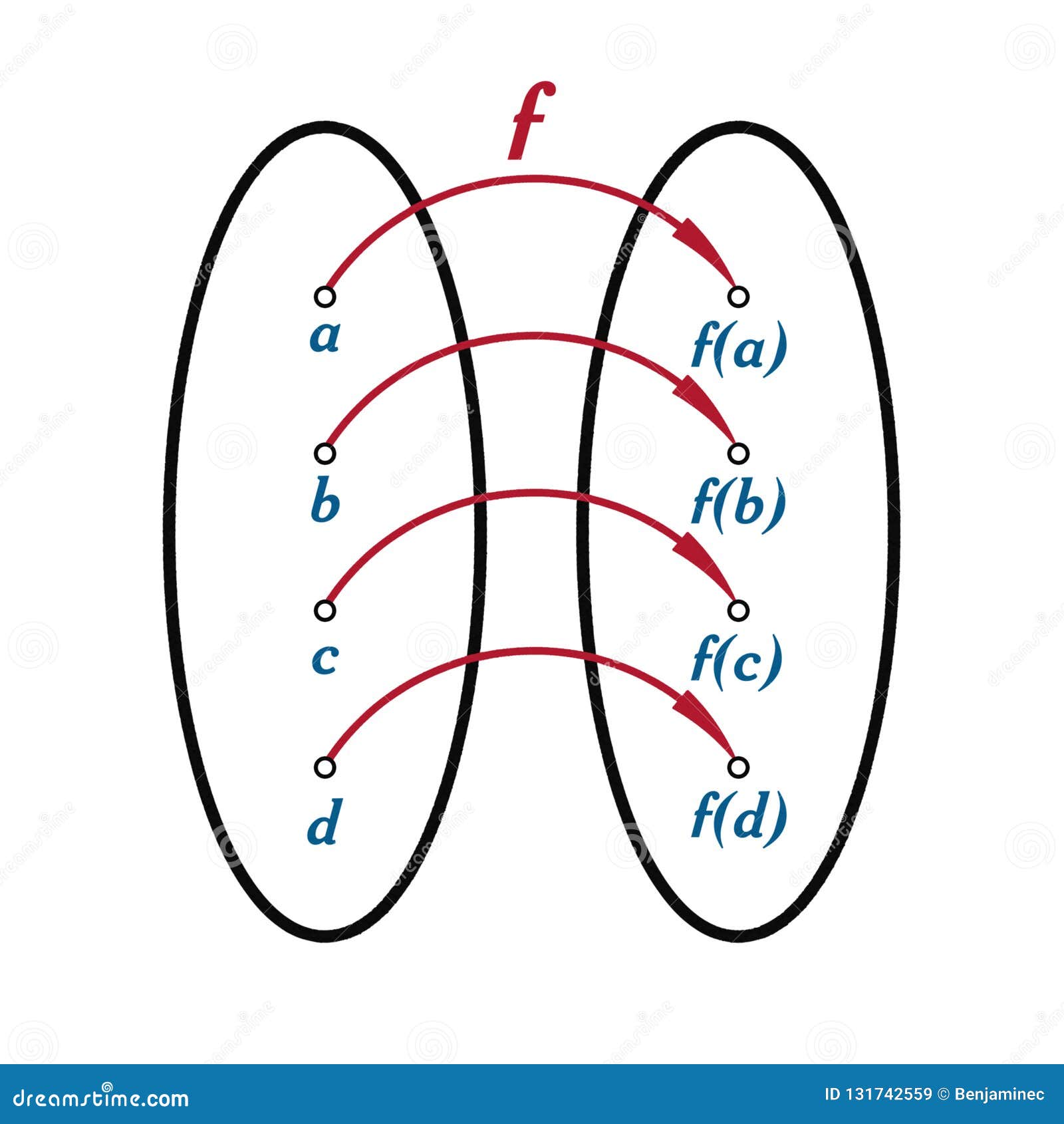
Une fonction f : X → Y est dite bijective ou est une bijection si pour tout y dans l’ensemble d'arrivée Y il existe un et un seul x dans l’ensemble de définition X tel que f ( x ) = y. On.

Une application définie sur un intervalle I à valeurs dans J est bijective ⇔ elle est continue et strictement monotone sur I. Une application définie sur un intervalle I à valeurs dans J.

Sais-tu comment montrer qu'une fonction est bijective ? En gros, sais-tu ce que signifie le terme "bijective" ? Une fois que tu as montrer la bijection, tu peux exprimer.

3. Fonction bijective. Une fonction f de E dans F est dite BIJECTIVE si elle est injective et surjective. NOTE : 1. Une application injective (resp. surjective, bijective) est.

Pour montrer qu'une fonction est bijective, on peut montrer qu'elle est continue et strictement monotone (Condition suffisante mais pas nécessaire !) Pour.

Re : Montrer qu'une fonction n'est pas bijective Si ton objectif est de montrer que f n'est pas bijective, il suffit de montrer que f n'est pas injective OU que f n'est pas surjective.. Par.

Après les fonctions injectives, on s'attaque aux fonctions surjectives ! Programme : * Qu'est ce qu'une fonction surjective ?* Quelle méthode utiliser pour a...

Salut, pour prouver qu'une fonction est bijective, on est d'accord que la méthode de base est de montrer qu'elle est injective et surjective. Certaines fois, il est.

Cours à l'ESCP 👨‍🏫 : https://www.cogitamusmaths.com/cours-collectifs🚩 Site officiel : https://www.cogitamusmaths.com 🚩📚 Cours particuliers : https ...

Une fonction h est dite bijective si et seulement si elle est et injective et surjective. En notation mathématique, on a ∀ 1, 2 ∈𝑑𝑜𝑚 ∶ = 1 2 ⇒ 1 = 2 𝑬𝑻 ∀ ∈ 𝑚 ( ∃ | = ) Remarque(s) Une.

Pour démontrer qu'une application f:E →F f: E → F est bijective, on peut. démontrer qu'elle est injective et surjective; démontrer que, pour tout y∈ F y ∈ F, l'équation y=f (x) y = f ( x).

Bonjour. comme d'habitude : on choisit un élément de l'ensemble d'arrivée quelconque, et on vérifie qu'il est l'image d'un et un seul couple de l'ensemble de départ..

Montrer qu’une fonction f : I \to \R strictement monotone est injective. Corrigé : Quitte à considérer - f , on peut supposer que f est strictement croissante. La.

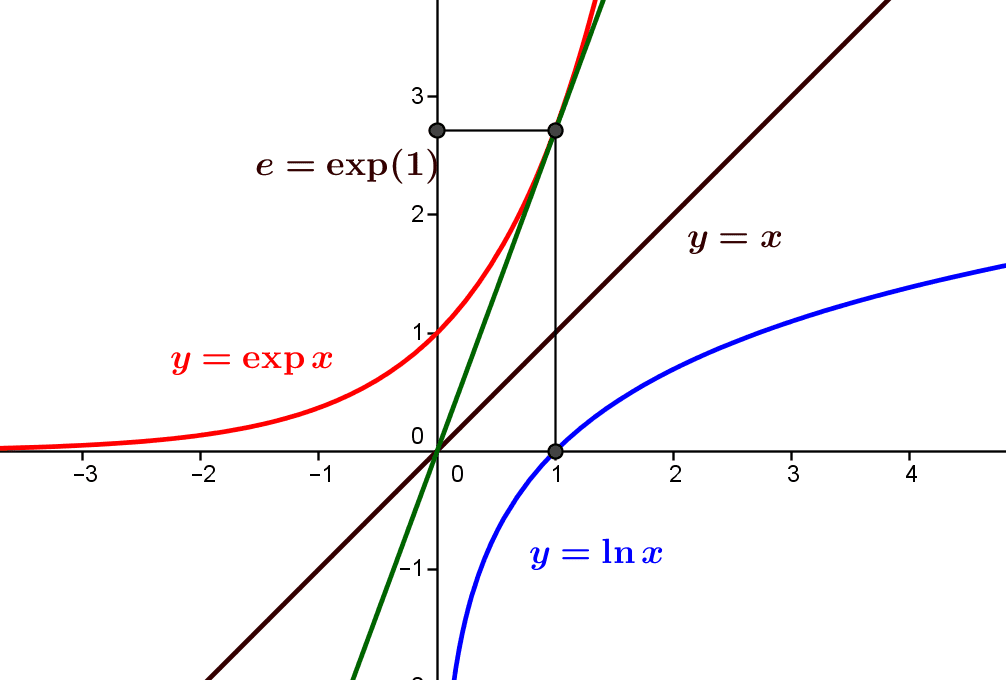
Comment montrer qu’une fonction complexe est bijective? Pour prouver qu’une fonction est bijective il suffit d’exhiber sa réciproque. Ici cela revient à résoudre.

Re : Montrer la bijectivité d'une fonction. Bonjour. Elle est valable pour des fonctions continues strictement monotones telles que l'image de l'ensemble de départ.

Comment montrer qu'une fonction de plusieurs variables est bijective ? Une fonction est bijective si a chaque image y par l'application de f n'a qu'un unique antécédent x. On.

J'ai un problème pour démontrer que la fonction f transformant x en x/(1+valeur absolue de x), de R à R, est une fonction bijective sur ]-1;1[. Je pensais.

Montrer Qu'une Fonction Est Une Bijection | Tutoriels

Vous pourriez aussi aimer

• Player Who Returned 10000 Years Chapter 31
• The Constellations Are My Disciples 28
• Jujutsu Kaisen Chapitre 64 Vf
• Page De Garde Cahier D écrivain Gs
• My Hero Academia 2: Note De Héros
• Branchement Interrupteur Legrand Neptune Va Et Vient
• Seducing The Monster Duke Manga
• The Game I Came From Manga
• Remettre Un Zirconium Sur Une Bague Prix
• Auto Hunting With My Clones 42
• My School Life Pretending To Be A Worthless Person
• Pages De Garde Cahier Mémoire
• Salle De Bain Italienne
• Coupe De Cheveux Garcon 13 Ans
• The Villainess Days Are Numbered
• One Piece 1087 Bleach Mx
• Compagnon Philippe Coelho Architecte Anne Elisabeth Lemoine
• Tensei Shitara Slime Datta Ken Ch 108
• Comment Demonter Un Pneu De Tracteur Tondeuse
• Kaoru Hana Wa Rin To Saku Characters