Tetraedru Regulat Formule

Salut les amis! On va explorer ensemble un coin fascinant de la géométrie : le tétraèdre régulier. Ne vous laissez pas intimider par le nom, c'est beaucoup plus simple et amusant qu'il n'y paraît! Comprendre les formules du tétraèdre régulier, c'est un peu comme débloquer un super-pouvoir pour résoudre des énigmes spatiales et briller en géométrie.
Alors, c'est quoi le but? Le tétraèdre régulier est un solide composé de quatre triangles équilatéraux identiques. Les formules nous permettent de calculer des choses comme le volume, l'aire de surface, et même la hauteur, en connaissant simplement la longueur d'un côté. L'avantage principal, c'est la simplicité! Une seule mesure de côté, et hop, on peut tout déduire!
Prenons un exemple concret. Imaginez que vous construisez une petite tente triangulaire pour vos figurines. Vous voulez savoir combien de tissu il vous faut (l'aire) et quel volume d'air il y aura à l'intérieur. Si chaque côté de votre tente triangulaire mesure 10 cm, les formules du tétraèdre régulier vous aideront à répondre à ces questions en un clin d'œil!
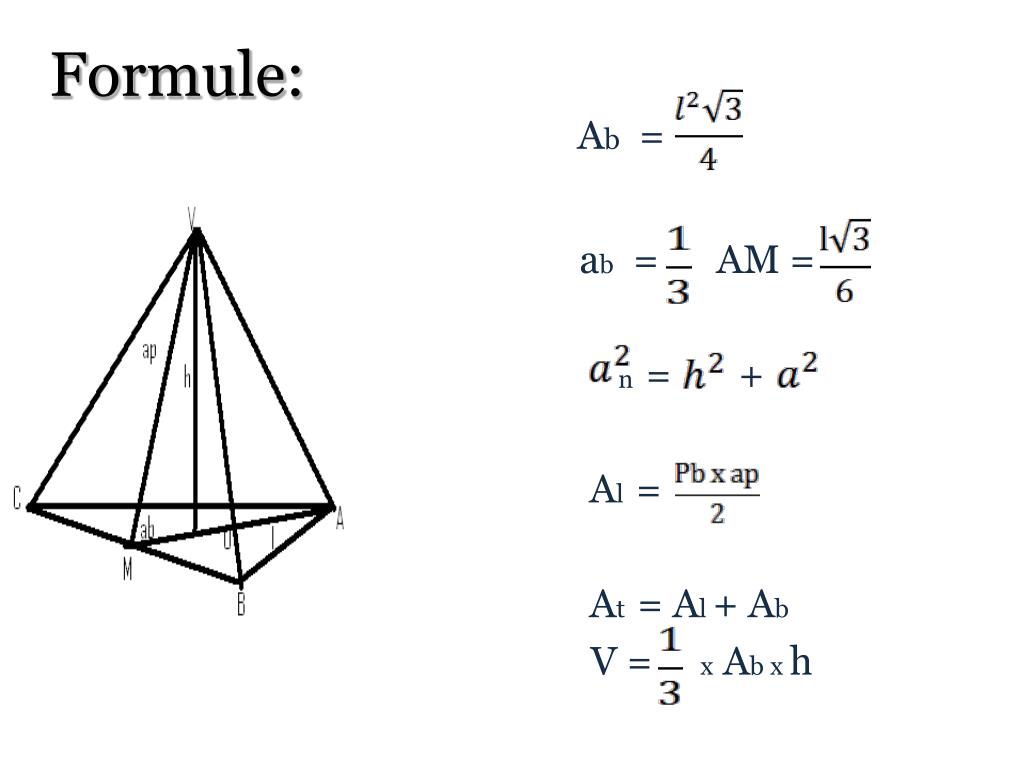
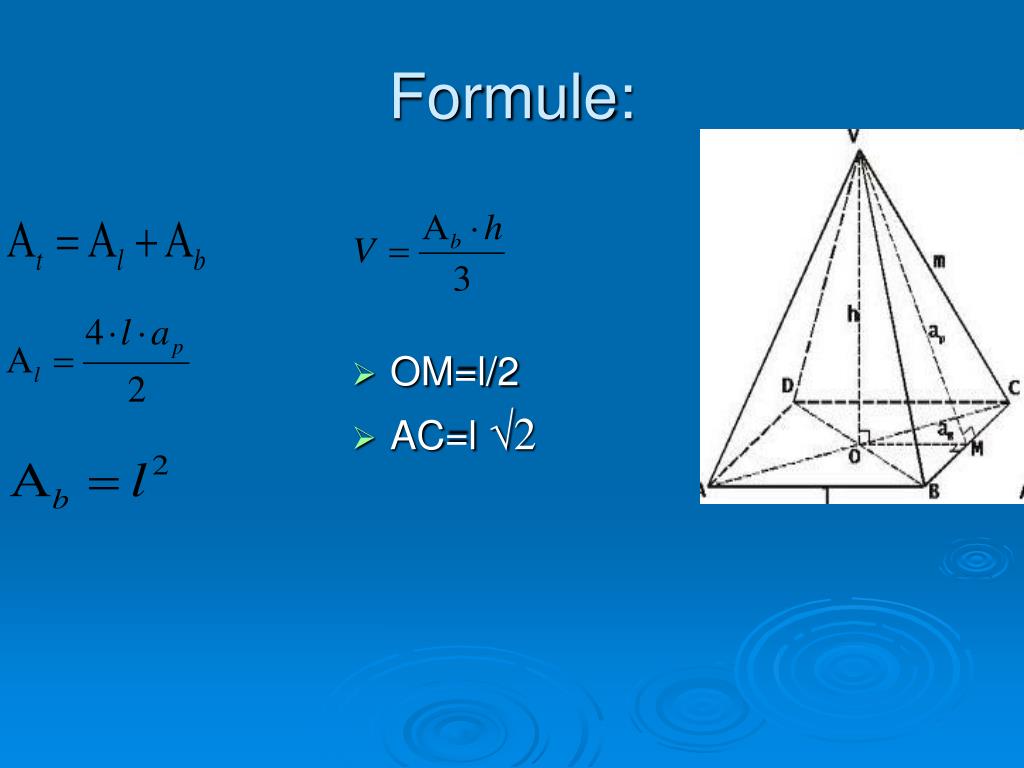
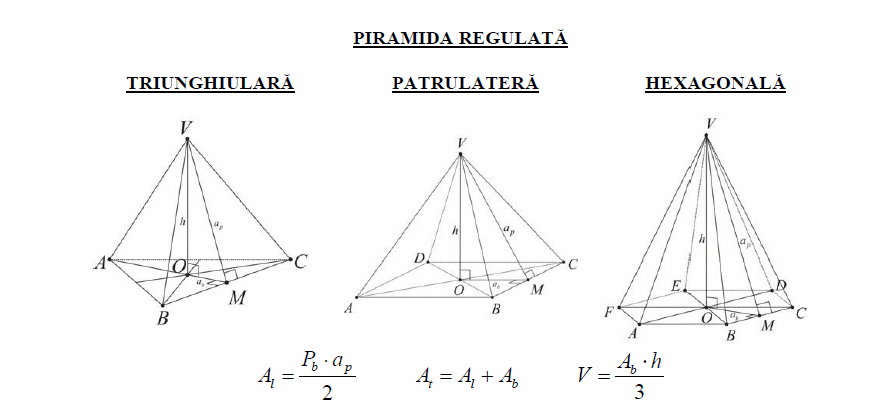
Voici quelques formules clés pour se lancer:
- Volume (V): V = (a³√2) / 12, où 'a' est la longueur d'un côté.
- Aire (A): A = √3 * a², où 'a' est la longueur d'un côté.
Un petit conseil : pour vous entraîner, dessinez des tétraèdres réguliers de différentes tailles. Calculez leur volume et leur aire. Vous pouvez même découper les patrons et les assembler pour visualiser concrètement ces formes géométriques! C'est une excellente façon d'intégrer les formules.
Et voilà! Vous avez maintenant les bases pour maîtriser le tétraèdre régulier. N'hésitez pas à explorer davantage, à chercher des exercices en ligne et à vous amuser avec la géométrie. À bientôt pour de nouvelles aventures mathématiques!